Since today is Pi day, let's use C# to calculate the value of Pi. There are several ways to calculate Pi out to a number of decimal points. Some are more or less complicated than others, and some are faster or slower than others.
The following method seems to be a solution that can be readily understood with some basic math.
From basic math we know that the area of a circle can be found with this formula: A = πr2, where r is the radius of the circle.
For a circle with radius 1 when then have A = π, and for one fourth of a circle we know A/4 = π/4. We'll use this fact in a moment.
From a little bit more math we know that the equation for a circle is x2 + y2 = 1. Solving for y, this becomes y = sqrt(1 + x2)
Now let's graph this equation. When we do so and consider the values from 0 to 1, it looks like this:
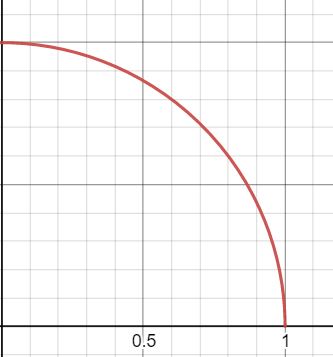
We have a quarter of a circle. Above we showed that A/4 = π/4, so if we can calculate the area of a quarter of a circle, we then know π/4, which we can multiply by 4 to get π.
So how do we get that area (without using π - since we are trying to derive π)?
Well with a bit more math, some basic calculus, we can do so. Remember that the basic idea of calculus is that we can approximate the area under a curve by breaking the area down into a series of rectangles that fit under the curve, and then summing up their areas. Then, if we keep using more and more rectangles of smaller width, we get a better approximation, and we converge on the area under the curve.
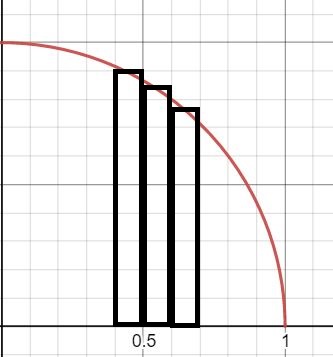
This type of iterative calculation lends itself nicely to a short computer program.
Here is the code to perform the above described logic. Comments describe the logic for each step:
using System;namespace CalcPi
{class Program{static void Main(String[] argv){// total area for our quarter circle, which equals pi divided by 4double totalArea = 0; // the bigger the value, the better our estimate of pilong numberOfRectangles = 1000000000;// width of one rectangle is the width of our area - 1 unit - divided by the number of rectangles we are going to split it intodouble widthOfRectangle = 1 / (double)(numberOfRectangles);// sum up the areas of all our rectanglesfor (long i = 0; i < numberOfRectangles; i++){double xValueOfCurrentRectangle = ((double)i + .5d) * widthOfRectangle; //add .5 because we want to calculate the height from the "middle" of the rectangle, not the left edgedouble heightOfCurrentRectangle = Math.Sqrt(1 - xValueOfCurrentRectangle * xValueOfCurrentRectangle); // from y = sqrt(1 - x^2)totalArea += widthOfRectangle * heightOfCurrentRectangle; // area of rectangle = base * height}// multiply by 4 to get the total area. since the radius of our circle is 1, this is the approximation of pitotalArea = totalArea * 4;Console.WriteLine("Pi is approximately: " + totalArea);}}
}
This will calculate Pi accurately out to 10 decimal places on my PC. If I start using more than 1,000,000,000 rectangles in the above code, the program begins to take a couple of seconds to run, versus running almost immediately.
Note that since each step of the calculation is independent of the other steps, this code would be well suited for parallel execution. For example, more rectangles could be used but then the workload could be distributed across several cores - core 1 could process rectangles 0 - 1,000,000,000, and core 2 could process 1,000,000,001 - 2,000,000,000, etc.